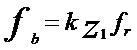Введение.

Рабочее колесо – основной и наиболее сложный узел центробежного нагнетателя (насоса или компрессора), характеризующийся рядом особенностей:

• Геометрия колеса весьма разнообразна и конструктивно отличается от устройства остальных элементов проточной части. Кроме того, конструкция межлопаточного канала сама по себе имеет сложную трехмерную структуру. Значительная часть наблюдаемых эффектов вызвана влиянием кривизны канала.
• Течение в колесе имеет турбулентный характер, число Рейнольдса может составлять 10000 – 1000000 при использовании разных конструкций.
• Главная особенность течения в рабочем колесе – вращение, при этом параметр вращения может достигать высоких значений.

Детальное знание особенностей потока в рабочем колесе позволяет разработать более эффективную конструкцию с меньшими потерями. Однако долгое время из-за недостаточных возможностей вычислительной техники трехмерная структура потока изучалась только экспериментальными методами. Сложность существовавших ранее промышленных устройств (высокие скорости и температуры) затрудняла даже экспериментальные измерения, и приходилось проводить их на модельных установках (несжимаемая жидкость, медленное вращение). Развитие вычислительной техники позволило перейти к численному моделированию, вначале по упрощенным двумерным моделям с использованием специально разработанных методов расчета средних характеристик потока, а затем и к полностью трехмерным расчетам.

Обращение к численному моделированию течения в рабочем колесе требует постановки задачи в трехмерной области сложной геометрии. При использовании структурированных сеток, как правило, возникает необходимость в использовании нескольких блоков. Требуется модель турбулентности и адекватный учет значительного влияния силы. Сложной задачей является и постановка граничных условий. И если описание твердых границ и поверхностей симметрии, в принципе, очевидно, то вид условий (профиля скорости) на входе в расчетную область не всегда известен из условий физического эксперимента, с которым сопоставляется расчет. Вместе с тем, поведение потока на входном участке определяет многие его дальнейшие свойства. [1]

Основные цели расчёта.

В данной работе рассматривается задача численного моделирования нестационарного течения в центробежном насосе. Моделирование проводится в рамках уравнений несжимаемой жидкости с учётом турбулентности и вязкости. На примере данного течения исследуется влияние различных моделей турбулентности на поведение параметров рабочего тела в выходном сечении центробежного насоса. При математическом моделировании в данной задаче граничные условия и условия сопряжения между ротором и статором выбраны таким образом, что расчёт происходит во всей области проточного тракта турбомашины, это даёт возможность учёта окружной неравномерности и нестационарности потока, что в свою очередь приближает результаты математического расчёта к реальным условиям рабочего процесса в центробежном насосе.

Параметры на выходе из рабочего колеса являются важнейшими и определяющими для оценки эффективности турбомашин и нестационарности рабочего процесса. Сравниваются результаты расчётов, проведённых при следующих режимах: стандартная k-e модель турбулентности, SA (Spalart-Allmaras) модель, SST (Shear Stress Transport) модель. Исследуются окружные, меридиональные и осевые компоненты скорости на входе и выходе из рабочего колеса, поле давления и поле скоростей в роторе, а также вблизи лопаток РК. Используя выходные параметры насоса, проводится расчёт и исследование пульсаций давления на выходе из насоса, амплитудно-частотного спектра давления.

Описание геометрии и модели, используемых в задаче.

Рабочим телом является воздух с параметрами идеального газа.

Геометрическая модель состоит из 3 Подобластей: «Inlet», «Rotor» и «Stator». На поверхностях каждой из подобластей были заданы соответствующие граничные условия.

На входе в подобласть «Inlet» – условие Входа/Выхода с нулевым давлением и нулевыми начальными параметрами завихренности  потока (пульсации = 0, масштаб турбулизации = 0), . На стенках данной подобласти – граничное условие стенки с логарифмическим профилем скорости у стенки.

«Inlet» и «Rotor» сопряжены между собой граничным условием скользящая поверхность на выходе из «Входа» и входе в «ротор» соответственно.

В подобласти «Ротор» задано движение в абсолютной системе координат – вращение с угловой скоростью 1500 оборотов в минуту.

На всех поверхностях выбрано граничное условие вращающейся стенки с логарифмическим профилем скорости у стенки, за исключением поверхности на выходе из подобласти, сопряженной со «Статором» граничным условием – скользящая поверхность.

На выходе из подобласти «Статор» задано условие – Входа/Выхода с указанием нормальной скорости (V = 0,876 м/с)

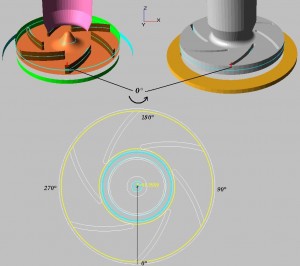
В дальнейшем при рассмотрении различных составляющих скорости по периметру окружности в сечении рабочего колеса турбомашины в качестве оси, вдоль которой откладываются значения величин, используется угол поворота относительно положения «угол» = 0°.

Значения координат, откладываемых относительно нулевого угла приведены на рисунке 1.

Начальная расчетная сетка задаётся неравномерной 37х37х30. В данной задаче требуется измельчение сетки на лопатках ротора и близи рабочего колеса, для этой цели расчётная сетка адаптирована до 2 уровня во всей подобласти «Rotor».

Шаг по времени задан неявным методом равным 0,001 секунды.

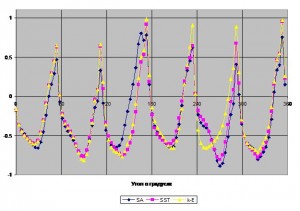
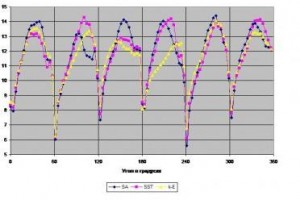
Рис. 2 Осевая составляющая скорости на входе в РК турбомашины

Рис. 3 Осевая составляющая скорости на выходе из РК турбомашины

Рис. 4 Радиальная составляющая скорости на входе в РК турбомашины

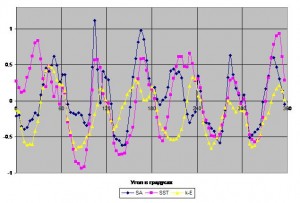
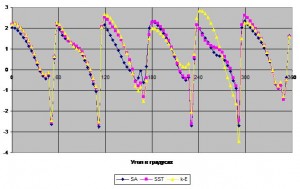
Рис. 6 Тангенциальная составляющая скорости на входе в РК турбомашины

Рис. 7 Тангенциальная составляющая скорости на выходе из РК турбомашины

Пульсации давления.

Пульсации давления в проточной части насосов, вентиляторов и других лопаточных машин возникают вследствие различных нестационарных гидродинамических явлений. Исследования динамических параметров насосов, вентиляторов показывают, что максимальные амплитуды в спектрах пульсаций давления и вибрации на расчетных режимах имеют дискретные составляющие на частотах следования лопаток рабочего колеса (ЧСЛ). [2]

– частота вращения ротора, Гц;

— число лопаток рабочего колеса;

– номер гармоники.

При расчёте данного модельного насоса (турбомашины) частота вращения ротора () составляла 1500 об/мин (25 Гц), а на рабочем колесе располагалось 6 лопаток ( = 6). В результате расчёта получили частоту следования лопаток РК турбины равной 150 Гц.

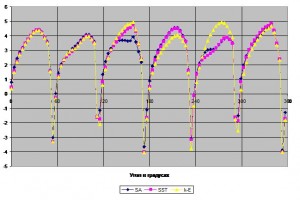
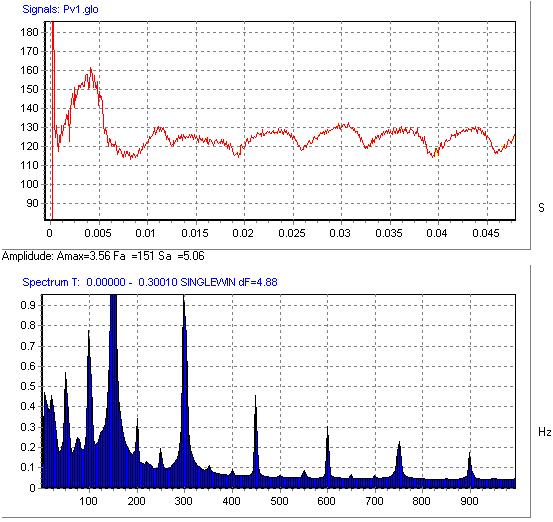
На графиках отчётливо видно, что максимальные значения амплитуды пульсаций давления соответствуют частоте первой гармоники (k=1), это значения А = 3,56 (k-e), 3,878 (SA), 3,83 (SST). Далее амплитуда пульсаций постепенно уменьшается, но, как было сказано выше, соответствует частотам, кратным ЧСЛ (300, 450, 600, 750, 900 Гц).

Рис. 8 Пульсации давления на выходе из РК (стандартная k-e модель)

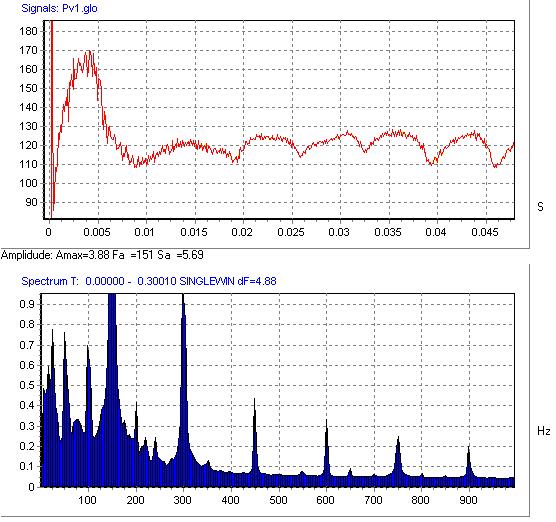Рис. 9 Пульсации давления на выходе из РК (SA (Spalart-Allmaras) модель) 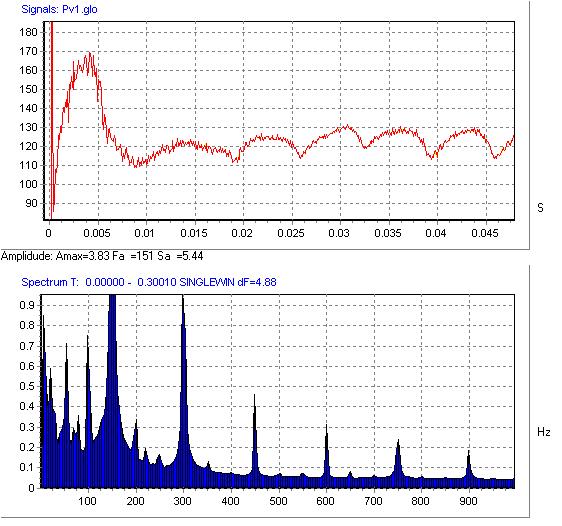Рис. 10 Пульсации давления на выходе из РК (SST (Shear Stress Transport) модель)

Заключение. Проведены расчёты течения в модельном насосе с учётом нестационарности процесса. В 3 расчётных вариантах начальные и граничные условия, а также параметры и методы расчёта были идентичны, за исключением модели турбулентности выбранной для течения. Полученные результаты позволяют сделать выводы о том, какая из представленных моделей турбулентности в пакете FlowVision, наиболее правдоподобно моделирует характер течения и его параметры. Основываясь на приведённые данные по составляющим скорости на входе и выходе из ротора и пульсации давления в выходном сечении центробежной турбомашины, можно сделать  предположение, что изменение модели турбулентности в данной конкретной задаче не приводит к значительным изменениям выходных параметров модельного насоса. В дальнейшем акустический расчёт мог бы стать продолжением работы по изучению процесса течения в центробежных компрессорах и насосах. Работа выполнена при частичной поддержке грантами РФФИ № 06-08-00005-А, № 06-08-03016-Б. Литература

1. А. М. Левченя «Численное моделирование турбулентного течения в рабочем колесе центробежного нагнетателя» Магистерская диссертация, Санкт-Петербургский Государственный Технический Университет, Физико-Механический факультет, Кафедра гидроаэродинамики, Санкт-Петербург, 2001, http://hotlinks.ru/private/diplom/
2. С. Ф. Тимушев «Применение акустико-вихревого метода к моделированию пульсаций давления и шума в лопаточных машинах с дозвуковым течением» Сборник докладов XVI сессии Российского акустического общества Москва, 14-18 ноября 2005 года, т.3, стр.209-213